Self-Attention

Since its introduction via the original transformer paper “Attention is all you need”, self-attention has become the corner stone of many state-of-the-art deep learning models, specially in the field of NLP. Self-attention mechanisms enable models to weigh different parts of input data differently, focusing on the most relevant information while performing a task. This mimics the human ability to selectively pay attention to certain aspects of our surroundings while filtering out distractions. Attention mechanisms have been instrumental in improving the performance of various AI models, particularly in sequence-to-sequence tasks.

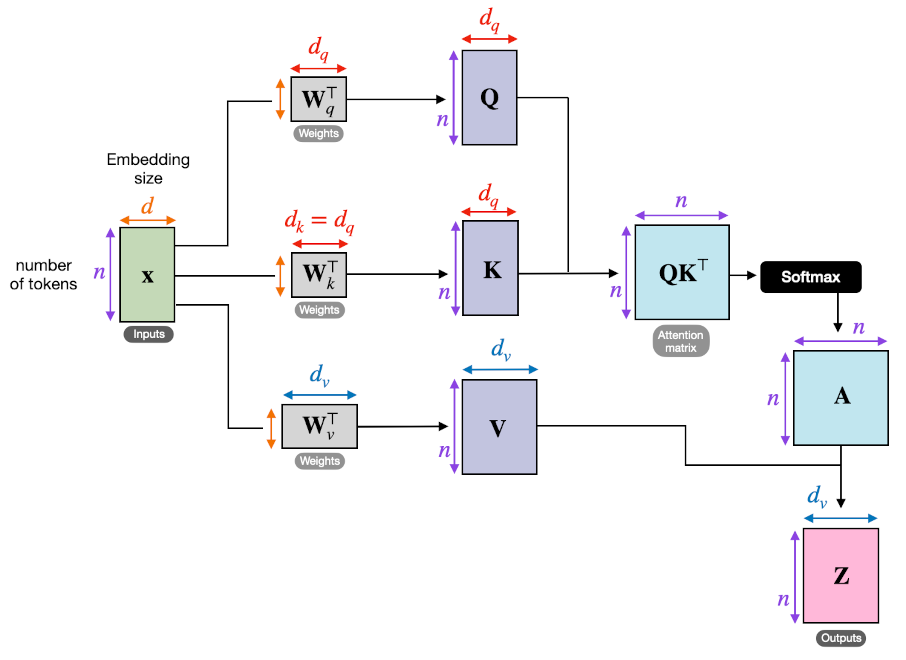
In a transformer architecture, “query”, “key” and “value” are the fundamental components used for calculating the self-attention. In simple terms, suppose we have a book related to animals; query represents the question that one might have such as “what is the largest mammal on earth?”. Similarly, key represents the index or table of content in the book and value represents the actual answer that we obtain from the book, in this case “blue whale”. In technical terms;. Query: A query is a matrix that represents the current token of request in the input sequence. Each word in the sequence has an associated query vector. 2. Key: A key is also a matrix that represents the content or identity of each token. 3. Value: A value is the actual information of each token that can be passed along.

For each token in the input sequence; the self-attention model computes query vector from it, computes key and value vectors from every token in the sequence, calculates attention score by taking dot product of query and each key, applies softmax and finally computes the output as the weighted sum of the value vectors.

Self-attention calculation

Mathematics of self-attention

Learnable Projections

Three trainable weight matrices, transform ( X ) into queries ( Q ), keys ( K ), and values ( V ):

\[Q = X \cdot W^Q, \quad W^Q \in \mathbb{R}^{d \times d_k}\]

\[K = X \cdot W^K, \quad W^K \in \mathbb{R}^{d \times d_k}\]

\[V = X \cdot W^V, \quad W^V \in \mathbb{R}^{d \times d_v}\]

Where: - \(( d_k )\): dimension of queries/keys - \(( d_v )\): dimension of values

Scaled Dot-Product Attention

Step 1: Compute Attention Scores

Compute all pairwise “compatibility” scores between queries and keys \[scores_{i,j} = Q_i \cdot K_j^T \in \mathbb{R}^{n \times n}\]

Step 2: Scale Scores

Because the magnitude of dot products grows with dimension \({d_k}\), we divide by \({\sqrt{d_k}}\): \[scaled_scores_{i,j} = \frac{scores_{i,j}}{\sqrt{d_k}}\]

Step 3: Softmax Normalization

For each query i, we want to convert its scores scaled_scores into a probability distribution over the N keys: \[A_{i,j} = softmax(scaled_scores_{i,j}), \quad A_{i,j} = \frac{e^{s_{i,j}}}{\sum_{k=1}^n e^{s_{i,k}}}\]

Step 4: Weighted Sum of Values

\[Output (O_i) = A_{i,j} \cdot V_j \in \mathbb{R}^{n \times d_v}\]

Self-attention implementation in CPU

Below is a step-by-step code walkthrough of C implementation that runs entirely on CPU.

High-level structure: * Allocate and initialize input query/key/value matrices (query, key, value). * Compute the attention scores attentionScores = Q × Kᵀ (with loops). * Apply scaling + row-wise softmax to produce softmaxedScores. * Compute output = softmaxedScores × V.

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

#define NUM_SAMPLES 2
#define FEATURE_DIMENSION 3

void printMatrix(float *matrix, int row, int col) {
    for (int i = 0; i < row; i++) {
        for (int j = 0; j < col; j++) {
            printf("%f ", matrix[i * col + j]);
        }
        printf("\n");
    }
}

// CPU Implementation of Attention
void transposeMatrix(float *in_matrix, float *out_matrix, int row, int col) {
    for (int i = 0; i < row; i++) {
        for (int j = 0; j < col; j++) {
            out_matrix[j * row + i] = in_matrix[i * col + j];
        }
    }
}

void computeAttentionCPU(float *query, float *key, float *value,
        float *attentionScores, float *output) {
    float *transposeKey = (float*)malloc(FEATURE_DIMENSION * NUM_SAMPLES * sizeof(float));
    transposeMatrix(key, transposeKey, NUM_SAMPLES, FEATURE_DIMENSION);

    float scalingFactor = 1.0f / sqrt((float)FEATURE_DIMENSION);

    // Compute attention scores
    for (int i = 0; i < NUM_SAMPLES; i++) {
        for (int j = 0; j < NUM_SAMPLES; j++) {
            for (int k = 0; k < FEATURE_DIMENSION; k++) {
                attentionScores[i * NUM_SAMPLES + j] += query[i * FEATURE_DIMENSION + k] * transposeKey[k * NUM_SAMPLES + j];
            }
            attentionScores[i * NUM_SAMPLES + j] *= scalingFactor;
        }
    }

    // Softmax row-wise
    for (int row = 0; row < NUM_SAMPLES; row++) {
        float maxScore = attentionScores[row * NUM_SAMPLES];
        for (int col = 1; col < NUM_SAMPLES; col++) {
            if (attentionScores[row * NUM_SAMPLES + col] > maxScore) {
                maxScore = attentionScores[row * NUM_SAMPLES + col];
            }
        }
        float sumExp = 0.0f;
        for (int col = 0; col < NUM_SAMPLES; col++) {
            attentionScores[row * NUM_SAMPLES + col] = expf(attentionScores[row * NUM_SAMPLES + col] - maxScore);
            sumExp += attentionScores[row * NUM_SAMPLES + col];
        }
        for (int col = 0; col < NUM_SAMPLES; col++) {
            attentionScores[row * NUM_SAMPLES + col] /= sumExp;
        }
    }

    // Multiply by value matrix
    for (int i = 0; i < NUM_SAMPLES; i++) {
        for (int j = 0; j < FEATURE_DIMENSION; j++) {
            for (int k = 0; k < NUM_SAMPLES; k++) {
                output[i * FEATURE_DIMENSION + j] += attentionScores[i * NUM_SAMPLES + k] * value[k * FEATURE_DIMENSION + j];
            }
        }
    }

    free(transposeKey);
}

int main() {
    float query[NUM_SAMPLES * FEATURE_DIMENSION] = {
        1.0f, 0.0f, -1.0f,
        0.5f, 0.5f, 0.5f
    };

    float key[NUM_SAMPLES * FEATURE_DIMENSION] = {
        1.0f, 2.0f, 3.0f,
        4.0f, 5.0f, 6.0f
    };
    
    float value[NUM_SAMPLES * FEATURE_DIMENSION] = {
        1.0f, 1.0f, 1.0f,
        2.0f, 2.0f, 2.0f
    };

    float* output = (float*)malloc(FEATURE_DIMENSION * NUM_SAMPLES * sizeof(float));
    float* attentionScores = (float*)malloc(NUM_SAMPLES * NUM_SAMPLES * sizeof(float));
    computeAttentionCPU(query, key, value, attentionScores, output);

    printMatrix(output, NUM_SAMPLES, FEATURE_DIMENSION);

    free(output);
    free(attentionScores);

    return 0;
}

Naive self-attention implementation in CUDA

This naive approach simply offloads the same steps to GPU, but without any fancy shared-memory tiling. Each thread computes one element of the matrix multiply or one element of the output. This is not memory- or compute-optimal, but it’s the easiest way to see how we map loops to kernels.

#include <stdio.h>
#include <cuda_runtime.h>
#include <math.h>
#include <stdlib.h>

#define NUM_SAMPLES 5
#define FEATURE_DIMENSION 6

void printMatrix(float *matrix, int row, int col) {
    for (int i = 0; i < row; i++) {
        for (int j = 0; j < col; j++) {
            printf("%.3f ", matrix[i * col + j]);
        }
        printf("\n");
    }
}

// Kernel: Softmax
__global__ void softmaxKernel(float *scoreMatrix, float *softmaxMatrix) {
    int row = blockIdx.y * blockDim.y + threadIdx.y;
    if (row < NUM_SAMPLES) {
        float maxScore = -1e30f;
        for (int col = 0; col < NUM_SAMPLES; ++col) {
            maxScore = fmaxf(maxScore, scoreMatrix[row * NUM_SAMPLES + col]);
        }
        float sumExp = 0.0f;
        for (int col = 0; col < NUM_SAMPLES; ++col) {
            softmaxMatrix[row * NUM_SAMPLES + col] = 
                expf(scoreMatrix[row * NUM_SAMPLES + col] - maxScore);
            sumExp += softmaxMatrix[row * NUM_SAMPLES + col];
        }
        for (int col = 0; col < NUM_SAMPLES; ++col) {
            softmaxMatrix[row * NUM_SAMPLES + col] /= sumExp;
        }
    }
}

// Kernel: QK^T
__global__ void computeScoreKernel(float *queryMatrix, float *keyMatrix, float *scoreMatrix) {
    int row = blockIdx.y * blockDim.y + threadIdx.y;
    int col = blockIdx.x * blockDim.x + threadIdx.x;
    if (row < NUM_SAMPLES && col < NUM_SAMPLES) {
        float score = 0.0f;
        for (int d = 0; d < FEATURE_DIMENSION; ++d) {
            score += queryMatrix[row * FEATURE_DIMENSION + d] *
                keyMatrix[col * FEATURE_DIMENSION + d];
        }
        scoreMatrix[row * NUM_SAMPLES + col] = score / sqrtf(static_cast<float>(FEATURE_DIMENSION));
    }
}

// Kernel: Output = Softmax(QK^T) * V
__global__ void computeOutputKernel(float * softmaxMatrix, float *valueMatrix, float *outputMatrix) {
    int row = blockIdx.y * blockDim.y + threadIdx.y;
    int col = blockIdx.x * blockDim.x + threadIdx.x;
    if (row < NUM_SAMPLES && col < FEATURE_DIMENSION) {
        float result = 0.0f;
        for (int k = 0; k < NUM_SAMPLES; ++k) {
            result += softmaxMatrix[row * NUM_SAMPLES + k] *
                valueMatrix[k * FEATURE_DIMENSION + col];
        }
        outputMatrix[row * FEATURE_DIMENSION + col] = result;
    }
}

void computeAttention(float *queryMatrix_h, float *keyMatrix_h, float *valueMatrix_h, float *attnMatrix_h) {
    float size = NUM_SAMPLES * FEATURE_DIMENSION * sizeof(float);
    float size_temp = NUM_SAMPLES * NUM_SAMPLES * sizeof(float);

    float *queryMatrix, *keyMatrix, *valueMatrix, *attnMatrix, *scoreMatrix, *softmaxMatrix;

    // Device memory allocation
    cudaMalloc((void**)&queryMatrix, size);
    cudaMalloc((void**)&keyMatrix, size);
    cudaMalloc((void**)&valueMatrix, size);
    cudaMalloc((void**)&attnMatrix, size);
    cudaMalloc((void**)&scoreMatrix, size_temp);
    cudaMalloc((void**)&softmaxMatrix, size_temp);

    cudaMemcpy(queryMatrix, queryMatrix_h, size, cudaMemcpyHostToDevice);
    cudaMemcpy(keyMatrix, keyMatrix_h, size, cudaMemcpyHostToDevice);
    cudaMemcpy(valueMatrix, valueMatrix_h, size, cudaMemcpyHostToDevice);
    
    // Kernel initializations
    dim3 blockDim(16, 16, 1);
    dim3 gridDim((NUM_SAMPLES+blockDim.x-1)/blockDim.x, (NUM_SAMPLES+blockDim.y-1)/blockDim.y, 1);
    computeScoreKernel<<<gridDim, blockDim>>>(queryMatrix, keyMatrix, scoreMatrix);
    cudaDeviceSynchronize();

    dim3 softmaxBlockDim(16, 16, 1);
    dim3 softmaxGridDim((NUM_SAMPLES+softmaxBlockDim.x-1)/softmaxBlockDim.x, (NUM_SAMPLES+softmaxBlockDim.y-1)/softmaxBlockDim.y, 1);
    softmaxKernel<<<softmaxGridDim, softmaxBlockDim>>>(scoreMatrix, softmaxMatrix);
    cudaDeviceSynchronize();

    dim3 outputBlockDim(16, 16, 1);
    dim3 outputGridDim((NUM_SAMPLES+outputBlockDim.x-1)/outputBlockDim.x, (NUM_SAMPLES+outputBlockDim.y-1)/outputBlockDim.y, 1);
    computeOutputKernel<<<outputGridDim, outputBlockDim>>>(softmaxMatrix, valueMatrix, attnMatrix);
    cudaDeviceSynchronize();

    // Copy output from device to host
    cudaMemcpy(attnMatrix_h, attnMatrix, size, cudaMemcpyDeviceToHost);

    cudaFree(queryMatrix);
    cudaFree(keyMatrix);
    cudaFree(valueMatrix);
    cudaFree(attnMatrix);
    cudaFree(scoreMatrix);
    cudaFree(softmaxMatrix);
}

int main() {
    int size = NUM_SAMPLES * FEATURE_DIMENSION * sizeof(float);

    float *queryMatrix = (float *)malloc(size);
    float *keyMatrix = (float *)malloc(size);
    float *valueMatrix = (float *)malloc(size);
    float *attnMatrix = (float *)malloc(size);

    // Initialize matrix
    for (int i = 0; i < NUM_SAMPLES * FEATURE_DIMENSION; i++) {
        queryMatrix[i] = (float)(rand() % 50);
        keyMatrix[i] = (float)(rand() % 50);
        valueMatrix[i] = (float)(rand() % 50);
    }

    printf("\nQuery:\n");
    printMatrix(queryMatrix, NUM_SAMPLES, FEATURE_DIMENSION);

    printf("\nKey:\n");
    printMatrix(keyMatrix, NUM_SAMPLES, FEATURE_DIMENSION);

    printf("\nValue\n");
    printMatrix(valueMatrix, NUM_SAMPLES, FEATURE_DIMENSION);

    // Attention calculation
    computeAttention(queryMatrix, keyMatrix, valueMatrix, attnMatrix);

    // Print attention matrix
    printf("\nAttention matrix;\:\n");
    printMatrix(attnMatrix, NUM_SAMPLES, FEATURE_DIMENSION);

    // Free memory
    free(queryMatrix);
    free(keyMatrix);
    free(valueMatrix);
    free(attnMatrix);

    return 0;
}

  Cell In[2], line 22
    float maxScore = -1e30f;
                         ^
SyntaxError: invalid decimal literal

Optimized self-attention in CUDA

This approach uses tiled/shared-memory to speed up the 𝑄𝐾⊤ and the final softmax × V operations. By loading contiguous chunks (tiles) of the input matrices into shared memory, threads within a block can cooperatively reuse data, minimizing expensive global‐memory round trips.

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <cuda_runtime.h>

#define NUM_SAMPLES 5
#define FEATURE_DIMENSION 6
#define TILE_WIDTH 16

// Print utility
void printMatrix(const float* matrix, int rows, int cols) {
    for (int r = 0; r < rows; ++r) {
        for (int c = 0; c < cols; ++c) {
            printf("%.3f ", matrix[r * cols + c]);
        }
        printf("\n");
    }
}

// Kernel: compute Q * K^T (scores)
__global__ void scoreKernel(
    const float* __restrict__ query,
    const float* __restrict__ keyT,
    float* __restrict__ score) {
    __shared__ float sharedQ[TILE_WIDTH][TILE_WIDTH];
    __shared__ float sharedK[TILE_WIDTH][TILE_WIDTH];

    int tx = threadIdx.x;
    int ty = threadIdx.y;
    int bx = blockIdx.x;
    int by = blockIdx.y;

    int col = bx * TILE_WIDTH + tx;
    int row = by * TILE_WIDTH + ty;
    float acc = 0.0f;

    int phases = (FEATURE_DIMENSION + TILE_WIDTH - 1) / TILE_WIDTH;
    for (int p = 0; p < phases; ++p) {
        int qCol = p * TILE_WIDTH + tx;
        int kRow = p * TILE_WIDTH + ty;

        // Load Q tile
        if (row < NUM_SAMPLES && qCol < FEATURE_DIMENSION)
            sharedQ[ty][tx] = query[row * FEATURE_DIMENSION + qCol];
        else
            sharedQ[ty][tx] = 0.0f;
        // Load K^T tile
        if (col < NUM_SAMPLES && kRow < FEATURE_DIMENSION)
            sharedK[ty][tx] = keyT[kRow * NUM_SAMPLES + col];
        else
            sharedK[ty][tx] = 0.0f;
        __syncthreads();

        // Dot-product
        for (int i = 0; i < TILE_WIDTH; ++i) {
            acc += sharedQ[ty][i] * sharedK[i][tx];
        }
        __syncthreads();
    }

    if (row < NUM_SAMPLES && col < NUM_SAMPLES) {
        score[row * NUM_SAMPLES + col] = acc / sqrtf((float)FEATURE_DIMENSION);
    }
}

// Kernel: row-wise softmax
__global__ void softmaxKernel(
    const float* __restrict__ score,
    float* __restrict__ softmax) {
    int row = blockIdx.y * blockDim.y + threadIdx.y;
    if (row < NUM_SAMPLES) {
        float maxv = -1e30f;
        for (int c = 0; c < NUM_SAMPLES; ++c)
            maxv = fmaxf(maxv, score[row * NUM_SAMPLES + c]);
        float sum = 0.0f;
        for (int c = 0; c < NUM_SAMPLES; ++c) {
            float e = expf(score[row * NUM_SAMPLES + c] - maxv);
            softmax[row * NUM_SAMPLES + c] = e;
            sum += e;
        }
        for (int c = 0; c < NUM_SAMPLES; ++c)
            softmax[row * NUM_SAMPLES + c] /= sum;
    }
}

// Kernel: softmax * V
__global__ void outputKernel(
    const float* __restrict__ softmax,
    const float* __restrict__ value,
    float* __restrict__ output) {
    __shared__ float sharedS[TILE_WIDTH][TILE_WIDTH];
    __shared__ float sharedV[TILE_WIDTH][TILE_WIDTH];

    int tx = threadIdx.x;
    int ty = threadIdx.y;
    int bx = blockIdx.x;
    int by = blockIdx.y;

    int col = bx * TILE_WIDTH + tx;
    int row = by * TILE_WIDTH + ty;
    float acc = 0.0f;

    int phases = (NUM_SAMPLES + TILE_WIDTH - 1) / TILE_WIDTH;
    for (int p = 0; p < phases; ++p) {
        int sCol = p * TILE_WIDTH + tx;
        int vRow = p * TILE_WIDTH + ty;

        // Load softmax tile
        if (row < NUM_SAMPLES && sCol < NUM_SAMPLES)
            sharedS[ty][tx] = softmax[row * NUM_SAMPLES + sCol];
        else
            sharedS[ty][tx] = 0.0f;
        // Load V tile
        if (vRow < NUM_SAMPLES && col < FEATURE_DIMENSION)
            sharedV[ty][tx] = value[vRow * FEATURE_DIMENSION + col];
        else
            sharedV[ty][tx] = 0.0f;
        __syncthreads();

        // Dot-product
        for (int i = 0; i < TILE_WIDTH; ++i) {
            acc += sharedS[ty][i] * sharedV[i][tx];
        }
        __syncthreads();
    }

    if (row < NUM_SAMPLES && col < FEATURE_DIMENSION) {
        output[row * FEATURE_DIMENSION + col] = acc;
    }
}

// Host helper: transpose key
void transposeKey(const float* key, float* keyT) {
    for (int r = 0; r < NUM_SAMPLES; ++r)
        for (int c = 0; c < FEATURE_DIMENSION; ++c)
            keyT[c * NUM_SAMPLES + r] = key[r * FEATURE_DIMENSION + c];
}

int main() {
    size_t qSize = NUM_SAMPLES * FEATURE_DIMENSION * sizeof(float);
    size_t kTSize = NUM_SAMPLES * FEATURE_DIMENSION * sizeof(float);
    size_t sSize = NUM_SAMPLES * NUM_SAMPLES * sizeof(float);

    // Host allocations
    float *hQ = (float*)malloc(qSize);
    float *hK = (float*)malloc(qSize);
    float *hV = (float*)malloc(qSize);
    float *hKT = (float*)malloc(kTSize);
    float *hScore = (float*)malloc(sSize);
    float *hSoftmax = (float*)malloc(sSize);
    float *hOut = (float*)malloc(qSize);

    // Random init
    for (int i = 0; i < NUM_SAMPLES * FEATURE_DIMENSION; ++i) {
        hQ[i] = rand() % 50;
        hK[i] = rand() % 50;
        hV[i] = rand() % 50;
    }

    printf("\nQuery:\n"); printMatrix(hQ, NUM_SAMPLES, FEATURE_DIMENSION);
    printf("\nKey:\n");   printMatrix(hK, NUM_SAMPLES, FEATURE_DIMENSION);
    printf("\nValue:\n"); printMatrix(hV, NUM_SAMPLES, FEATURE_DIMENSION);

    // Transpose key on host
    transposeKey(hK, hKT);

    // Device allocations
    float *dQ, *dKT, *dV, *dScore, *dSoftmax, *dOut;
    cudaMalloc(&dQ, qSize);
    cudaMalloc(&dKT, kTSize);
    cudaMalloc(&dV, qSize);
    cudaMalloc(&dScore, sSize);
    cudaMalloc(&dSoftmax, sSize);
    cudaMalloc(&dOut, qSize);

    // Copy to device
    cudaMemcpy(dQ, hQ, qSize, cudaMemcpyHostToDevice);
    cudaMemcpy(dKT, hKT, kTSize, cudaMemcpyHostToDevice);
    cudaMemcpy(dV, hV, qSize, cudaMemcpyHostToDevice);

    // Launch score kernel
    dim3 block(TILE_WIDTH, TILE_WIDTH);
    dim3 gridScore((NUM_SAMPLES+TILE_WIDTH-1)/TILE_WIDTH,
                   (NUM_SAMPLES+TILE_WIDTH-1)/TILE_WIDTH);
    scoreKernel<<<gridScore, block>>>(dQ, dKT, dScore);
    cudaDeviceSynchronize();

    // Softmax kernel
    dim3 gridSm((NUM_SAMPLES+TILE_WIDTH-1)/TILE_WIDTH, 1);
    softmaxKernel<<<gridSm, block>>>(dScore, dSoftmax);
    cudaDeviceSynchronize();

    // Output kernel
    dim3 gridOut((FEATURE_DIMENSION+TILE_WIDTH-1)/TILE_WIDTH,
                 (NUM_SAMPLES+TILE_WIDTH-1)/TILE_WIDTH);
    outputKernel<<<gridOut, block>>>(dSoftmax, dV, dOut);
    cudaDeviceSynchronize();

    // Copy back
    cudaMemcpy(hOut, dOut, qSize, cudaMemcpyDeviceToHost);

    printf("\nAttention Output:\n");
    printMatrix(hOut, NUM_SAMPLES, FEATURE_DIMENSION);

    // Cleanup
    free(hQ); free(hK); free(hV); free(hKT);
    free(hScore); free(hSoftmax); free(hOut);
    cudaFree(dQ); cudaFree(dKT); cudaFree(dV);
    cudaFree(dScore); cudaFree(dSoftmax); cudaFree(dOut);

    return 0;
}

  Cell In[3], line 35
    float acc = 0.0f;
                  ^
SyntaxError: invalid decimal literal

Flash attention in CUDA

Flash Attention is a specialized, fused‐kernel approach that was introduced to compute softmax(𝑄𝐾⊤)𝑉 in a single (or a small number of) GPU kernels, without ever storing the full 𝑁×𝑁 attention matrix in DRAM. Instead, it computes partial dot products and partial softmaxes in registers or shared memory, blocking in both the 𝑁 (sequence length) and 𝑑 (feature) dimensions. This greatly reduces memory bandwidth and peak memory usage, making it possible to handle very large sequences on a single GPU.

#include <stdio.h>
#include <cuda_runtime.h>
#include <math.h>
#include <stdlib.h>

#define NUM_SAMPLES 5
#define FEATURE_DIMENSION 6

void printMatrix(float *matrix, int row, int col) {
    for (int r = 0; r < row; r++) {
        for (int c = 0; c < col; c++) {
            printf("%.3f ", matrix[r * col + c]);
        }
        printf("\n");
    }
}

// Kernel: Attention Score (x = QK^T)
__global__ void attention_score_kernel(
    float *Q, float *K, float *x
) {
    int row = blockIdx.y * blockDim.y + threadIdx.y;
    int col = blockIdx.x * blockDim.x + threadIdx.x;

    if (row < NUM_SAMPLES && col < NUM_SAMPLES) {
        float sum = 0.0f;
        for (int i = 0; i < FEATURE_DIMENSION; i++) {
            sum += Q[row * FEATURE_DIMENSION + i] * K[col * FEATURE_DIMENSION + i];
        }
        x[row * NUM_SAMPLES + col] = sum;
    }
}

// Kernel: Flash Attention
__global__ void flash_attention_kernel(
    float *x, float *V, float *O
) {
    int row = blockIdx.y * blockDim.y + threadIdx.y;
    int col = blockIdx.x * blockDim.x + threadIdx.x;

    if (row < NUM_SAMPLES && col < FEATURE_DIMENSION) {
        float m = -INFINITY;
        float d = 0.0f;
        float o = 0.0f;

        for (int i = 0; i < NUM_SAMPLES; i++){
            float x_val = x[row * NUM_SAMPLES + i];
            float m_prev = m;
            float d_prev = d;

            // Compute running max and denominator
            m = fmaxf(m_prev, x_val);
            d = (d_prev * expf(m_prev - m)) + expf(x_val - m);

            // Compute output
            float v_val = V[i * FEATURE_DIMENSION + col];
            o = o * ((d_prev * expf(m_prev - m)) / d) + (expf(x_val- m) / d) * v_val;
        }
        O[row * FEATURE_DIMENSION + col] = o;
    }
}

void computeFlashAttention(
    float *Q, float *K, float *V, float *O
) {
    float *d_Q, *d_K, *d_V, *d_x, *d_O;
    size_t size_1 = NUM_SAMPLES * FEATURE_DIMENSION * sizeof(float);
    size_t size_2 = NUM_SAMPLES * NUM_SAMPLES * sizeof(float);

    // Allocate device memory
    cudaMalloc((void**)&d_Q, size_1);
    cudaMalloc((void**)&d_K, size_1);
    cudaMalloc((void**)&d_V, size_1);
    cudaMalloc((void**)&d_x, size_2);
    cudaMalloc((void**)&d_O, size_1);

    // Copy data from host to device
    cudaMemcpy(d_Q, Q, size_1, cudaMemcpyHostToDevice);
    cudaMemcpy(d_K, K, size_1, cudaMemcpyHostToDevice);
    cudaMemcpy(d_V, V, size_1, cudaMemcpyHostToDevice);

    // Kernel launch for attention score
    dim3 blockDim(16, 16, 1);
    dim3 gridDim((NUM_SAMPLES + blockDim.x - 1)/blockDim.x, (NUM_SAMPLES + blockDim.y - 1)/blockDim.y, 1);
    attention_score_kernel<<<gridDim, blockDim>>>(d_Q, d_K, d_x);
    cudaDeviceSynchronize();

    // Kernel launch for flash attention
    dim3 blockDim2(16, 16, 1);
    dim3 gridDim2((NUM_SAMPLES + blockDim2.x - 1)/blockDim2.x, (NUM_SAMPLES + blockDim2.y - 1)/blockDim2.y, 1);
    flash_attention_kernel<<<gridDim2, blockDim2>>>(d_x, d_V, d_O);
    cudaDeviceSynchronize();

    // Copy Output from device to host
    cudaMemcpy(O, d_O, size_1, cudaMemcpyDeviceToHost);

    // Free device memory
    cudaFree(d_Q);
    cudaFree(d_K);
    cudaFree(d_V);
    cudaFree(d_x);
    cudaFree(d_O);
}

int main() {
    float size = FEATURE_DIMENSION * NUM_SAMPLES * sizeof(float);
    float *Q = (float *)malloc(size);
    float *K = (float *)malloc(size);
    float *V = (float *)malloc(size);
    float *O = (float *)malloc(size);

    // Initialize matrices
    for (int i = 0; i < NUM_SAMPLES * FEATURE_DIMENSION; i++) {
        Q[i] = rand() % 50;
        K[i] = rand() % 50;
        V[i] = rand() % 50;
    }
    printf("\nQuery:\n"); printMatrix(Q, NUM_SAMPLES, FEATURE_DIMENSION);
    printf("\nKey:\n");   printMatrix(K, NUM_SAMPLES, FEATURE_DIMENSION);
    printf("\nValue:\n"); printMatrix(V, NUM_SAMPLES, FEATURE_DIMENSION);

    // Compute Flash Attention
    computeFlashAttention(Q, K, V, O);
    printf("\nOutput:\n"); printMatrix(O, NUM_SAMPLES, FEATURE_DIMENSION);

    // Free host memory
    free(Q);
    free(K);
    free(V);
    free(O);

    return 0;
}

Explanation of Key Steps

• Single-Kernel Fusion: Unlike the naive version (which had 3 separate kernels: dot-product, softmax, matmul), Flash Attention does everything in one kernel launch.
• Shared Memory Usage for K and V: We load the entire 𝐾 and 𝑉 into shared memory once.
• Computing row_max and row_sum in a Streaming Fashion: We do a two-pass approach (but within the same kernel):
  • Pass 1: scan over all keys to find row_max.
  • Pass 2: scan again over all keys to accumulate row_sum = ∑ exp((QK)/√d – row_max). This two-pass trick avoids having to store all raw scores. We only keep track of two scalars per query.
• Computing Final Weighted Sum Over V: Once we know A𝑖,𝑗 we multiply by 𝑉𝑗. Since 𝑉𝑗 is already in shared memory (for that entire tile of keys), we can do this accumulation without accessing DRAM for every (𝑖,𝑗).

Why This Is “Flash” (Fast + Low Memory):

Fused Kernel means we only launch one CUDA kernel—no separate writes/reads of a big 𝑁×𝑁 attention-matrix. The partial dot products and exponentials are handled “on the fly” in registers or shared memory.